Силы притяжения, действующие на тело внутри диска [Петр Путенихин] (fb2) читать онлайн

Петр Путенихин Силы притяжения, действующие на тело внутри диска

1. Сила притяжения внутри диска

В результате астрономических наблюдений выяснилось, что звёзды на краю галактик движутся быстрее, чем этого требуют законы Кеплера. Скорости звёзд обобщённо описываются так называемой кривой вращения, то есть, зависимостью скорости объекта от его удалённости от центра галактики. Согласно кривым вращения, звёзды с такими скоростями попросту должны покинуть галактику, но этого не происходит.

Некоторые галактики представляют собой диск переменной толщины, напоминающий скорее спортивный снаряд — диск или две шляпы приложенные друг к другу. В общем случае такой диск галактики можно рассматривать как объект, имеющий разную плотность, в зависимости от удалённости от центра.

Далее мы рассмотрим гипотетическую структуру, некое условное подобие галактики: тонкий, с нулевой толщиной пылеобразный диск радиуса R₀, внутри которого находится точечное тело массой m. Никакой привязки к реальной галактике мы не делаем. Под пылеобразностью диска подразумевается возможность для тел, находящихся внутри него, беспрепятственно двигаться независимо от других его компонент.

Основной целью наших вычислений, исследований является определение возможности по заранее заданной произвольной кривой вращения сформировать такую функцию плотности, которая, собственно, и формирует эту кривую вращения. Если такая процедура возможна, то мнение о том, что движение звёзд на окраине галактик не-кеплеровское, следует, по меньшей мере, признать неточным. Также это будет означать, что такие скорости и вообще любые скорости напрямую связаны с функцией плотности дисковой галактики.

Вычислим силу, действующую на тело m внутри этого диска. Вычисления будем проводить, условно разбив диск на набор обручей, каждый из которых притягивает тело m независимо от других. На следующем рисунке радиус R₀— это радиус всего диска, внутри которого пробное тело m, для которого мы и вычисляем силы, находится на удалении Rx от центра. Считаем, что на пробное тело действуют две условные силы: сила, притягивающая его в центр, суммарная сила от обручей с радиусом, меньшим Rx, и ослабляющая её сила, направленная наружу, от центра диска. Эту ослабляющую силу, очевидно, создают внешние части обручей с радиусом, превышающим Rx. Внешние части обручей — это те, что находятся за координатой Rx.

Рис. 1.1. Сила притяжения между дифференциалом dM массы диска и пробным телом m внутри диска

Элементарная сила притяжения dF, создаваемая дифференциальным элементом любого обруча равна

Дифференциал массы обруча определяем через дифференциал площади ds, который равен

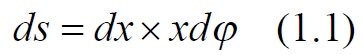
Расстояние r между массой m и дифференциальным элементом

Подставляем (1.1) и (1.2) в уравнение силы

Эта сила имеет две ортогональные составляющие — вдоль оси X и перпендикулярно ей. Перпендикулярные силы, в конечном счете, компенсируют друг друга вследствие симметрии. Нас же интересует только сила, направленная вдоль горизонтальной оси, формирующие общую силу притяжения m в сторону центра диска. Эта составляющая определяется из подобных треугольников

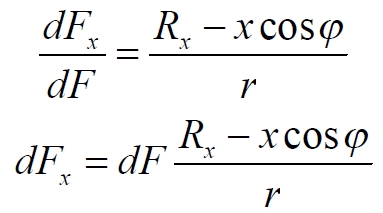
Подставляем величину силы

Преобразуем

Интегрированием по всему радиусу диска находим полную силу

Это и есть полное значение силы, действующей на m, которое находится в средней части диска. Отметим, что ослабляющая сила тем сильнее, чем ближе m к центру диска. Здесь следует отметить следующее. Рассмотрим сумму в скобках в числителе

При вычислениях интеграла величина x для некоторого положения тела Rx изменяется в интервале от 0 до R₀ — на полном интервале радиуса диска. Этот интервал x следует формально разделить на два участка. На первом участке всегда x ≤ Rx, на втором — всегда x > Rx. Это приводит к тому, что в первом случае величина (1.4) и соответствующий ей интеграл в (1.3) оказывается положительной величиной всегда, а во втором, при некоторых углах φ, величина (1.4) и соответствующий ей интеграл в (1.3) становятся отрицательными. На знак интеграла знаменатель влияния не оказывает, поскольку сумма квадратов величин всегда больше их удвоенного произведения. Действительно, максимальное значение отрицательного слагаемого, способного сделать эту сумму отрицательной, определяется значением косинуса. Максимум отрицательной величины очевиден — это единичное значение косинуса:

В этом случае получаем уравнение

То есть, мы получили величину, которая никогда не принимает отрицательных значений, следовательно, и (1.5) также всегда положительна. Это означает, что при значениях параметра x, для некоторых обручей диска, являющихся для m внешними, сила притяжения при определённых углах φ имеет отрицательные значения, то есть, уменьшает силу притяжения тела в сторону центра диска. Запишем окончательное уравнение для результирующей силы, действующей на пробное тело m

Выведенное интегральное уравнение позволяет построить кривую вращения по графику плотности вещества галактики. Для достижения поставленной цели, определения функции плотности по кривой вращения, нам, очевидно, нужна и функция этой кривой вращения.

Для большей наглядности в вычислениях мы будем использовать реальную кривую вращения — наблюдаемую кривая вращения галактики Млечный Путь. Функция этой кривой вращения представлена в табличном виде. Каждая кривая вращения является производной от силы притяжения и определяется из равенства этой силы силе центробежной

Силу притяжения нам позволяет вычислить наше интегральное уравнение (1.6), следовательно

Преобразуем уравнение (1.7)

Поскольку известной, вычисляемой величиной у нас является сила F, среднюю часть уравнений отбрасываем

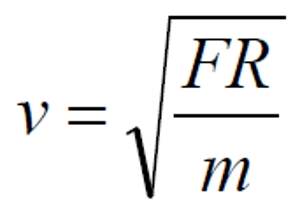
Здесь силой F является сила (1.6). Сделаем запись ещё короче, присвоив массе m единичное значение.

Это уравнение мы и будем использовать для построения кривой вращения, являющейся производной от функции плотности, поскольку сила F в уравнении (1.6) сама является функцией плотности. Заметим, что вывести обратную аналитическую зависимость — функции плотности от скорости вращения — задача, как оказалось, крайне сложная, если вообще разрешимая. Для решения поставленной задачи у нас, таким образом, остаётся только одно средство — итерация. Мы задаём некий закон, функцию плотности, по которой вычисляем кривую вращения, строим её график. Если этот график визуально, субъективно не совпадает с эталонным, корректируем функцию плотности и повторяем вычисления до тех пор, пока не будет достигнуто минимальное, приемлемое различие графиков.

2. Построение пробных диаграмм

Итак, мы вывели достаточно простое интегральное уравнение для построения сил, действующих на тело, помещённое внутрь пылевого диска с переменной плотностью. В процессе его исследования, построения кривых вращения для разных функций плотности были получены интересные, и даже, можно сказать, удивительные результаты.

Первая же графическая проверка сформированного интеграла сил показала довольно любопытный результат, которому можно привести достаточно логичное объяснение. Рассмотрим диаграмму сил притяжения тела, находящегося на разных удалениях от центра внутри однородного диска, диска с неизменной плотностью. Вычисления сделаны численным интегрирование уравнения (1.6) в "сдвоенном" режиме. В процессе интегрирования на диаграмму выводились два значения, по одному для каждого из двух графиков. Одно в момент равенства x = Rx, когда определено частичное значение интеграла, в котором переменная интегрирования x равна Rx, радиальной координате точки расположения тела m. Это значение интеграла, понятно, соответствует величине силы только от внутренних обручей. Второе значения интеграла — конечное, соответствует силе притяжения от всех обручей.

Рис. 2.1. Силы притяжения Fxo — только от внутренних обручей; Fx — от всех обручей; a) — равные масштабы; б) — график Fx в увеличенном масштабе

На верхнем рисунке, рис. 2.1a в равных масштабах приведены графики: Fx — график полной силы, с учётом внешних слоёв диска, Fxo — без учёта этих слоёв. Напомним, что для объекта m внешние слои диска — это условные обручи с радиусом, превышающим удалённость объекта от центра диска. Графики на рис. 2.1a полностью вписаны в диаграмму. На нижнем рисунке рис. 2.1б график Fx приведён в увеличенном масштабе. Как видим, на начальном участке график Fx уходит в минус. Это означает, что тело притягивается не к центру диска, а наружу, к его периферии, внутри обруча тело испытывает силу притяжения к его ближней части. Скачок графика Fx в самом начале координат может быть связан, например, с достаточно грубой дискретностью на начальном этапе. Действительно, окружность R_x радиусом в одну дискрету программой рассматривается не как окружность, а как прямоугольник со сторонами dx на πdx. Другой вариант объяснения пика — на начальном этапе, на малых дистанциях влияние внутренних сил диска выше, чем внешних. Проверить, что из этого верно, можно лишь увеличив точность вычислений в области центра диска.

На верхнем рисунке рис. 2.1a видно, что оба графика сошлись в одной точке. Это также объяснимо: на краю диска у притягиваемого тела нет вещества "за спиной", поэтому обе равные силы притяжения направлены в центр диска. Величина этой силы, очевидно, не должна зависеть от способа её вычисления.

График Fxo практически прямолинейный, то есть, сила притяжения к центру однородного диска тела, находящегося на его краю, прямо пропорциональна радиусу диска.

Рис. 2.2. Силы притяжения диска с гиперболической функцией плотности: Fxo — только от внутренних обручей; Fx — от всех обручей

Что интересно и даже удивительно, при учёте "внешних слоёв", обручей такого диска график силы Fx довольно долго растёт почти по закону параболы, а вблизи края диска — скорость роста резко возрастает. Это означает, что сила притяжения внешних частей диска наружу буквально "подавляет" силу притяжения внутренних дисков. Для сравнения построим график сил для диска с гиперболической функцией плотности, плотности, которая убывает от центра диска к его периферии — рис. 2.2.

Для такого частного, специфического распределения плотности диска кривая вращения приобрела вид, явно отличающийся от кеплеровского, рис. 2.3.

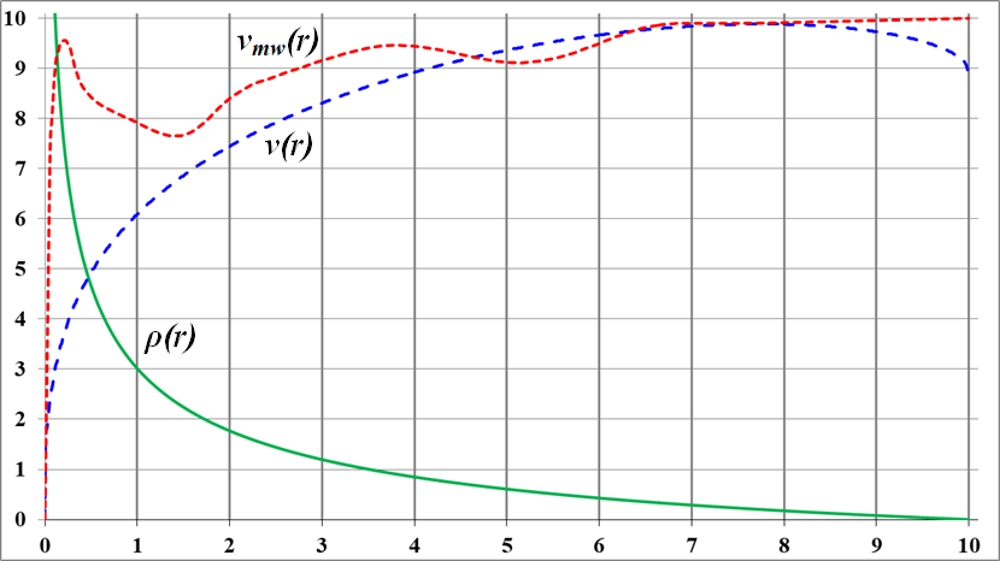
Рис. 2.3. Диск с гиперболической функцией плотности имеет кривую вращения, приближающуюся к наблюдаемой кривой вращения галактики Млечный Путь

Начальный участок графика плотности на рис. 2.2 и рис. 2.3 уходит по гиперболе далеко вверх. Его уравнение

Разумнее было предположить, что плотность ρ₀ неизменна не только в точке, а на некотором интервале начального участка, в центральной части диска. После корректировки, установки плотности ρ₀ на таком участке график приобрёл такой вид рис. 2.4.

Неизменное значение плотности было до r = 0,59 включительно. Внешнее, приблизительное сходство графика с кривой вращения Млечного Пути, несомненно. А если изменить плотность на другом интервале радиусов? Попытки точечного изменения плотности показали, что прямой, пропорциональной связи между графиком плотности и кривой вращения нет. Каждый изгиб графика плотности, изгиб в любой его точке приводит к изменению кривой вращения также и в других её точках.

Рис. 2.4. Диск с гиперболической функцией плотности и отсечённым верхом, максимумом имеет кривую вращения, довольно сильно приближенную к наблюдаемой кривой вращения галактики Млечный Путь

Рис. 2.5. Небольшой выступ на графике плотности ведёт к сильному искажению, всплеску на кривой вращения

Небольшая площадка в области r = 4,5 привела к довольно серьёзной деформации кривой вращения. Пробуем скачкообразно изменить плавность изменения плотности в конце графика, после r = 8.

Плотность была сформирована фактически из двух интервалов (скачок на 8). До 8 показатель степени в уравнении (2.1) n = 0,5, после 8 показатель n = 0,3. Пик на кривой вращения оказался весьма крутым. На графике силы Fx этот скачок существенно меньше, что объяснимо его квадратичной зависимостью. Заметим, что график плотности в конце диска имеет ненулевое значение.

Рис. 2.6. Ступенька на графике плотности ведёт к сильному искажению, пику на кривой вращения

Считая, это не совсем верно, вносим небольшую корректировку в уравнение плотности, сделав её значение на краю диска равной нулю

Формируем новый интервал n = 0,45 после r = 8 и строим диаграммы. Скачок привел к немного уменьшенному эффекту, но по-прежнему с заметным пиком на кривой вращения.

Рис. 2.7. Пик на кривой вращения возникает при любой, даже самой малой ступеньке на графике плотности

Эффекты явно вызваны скачком плотности. Пробуем заменить скачок в r = 8 плавным переходом и для сравнения добавляем скачки на r = 5 и на r = 9,2.

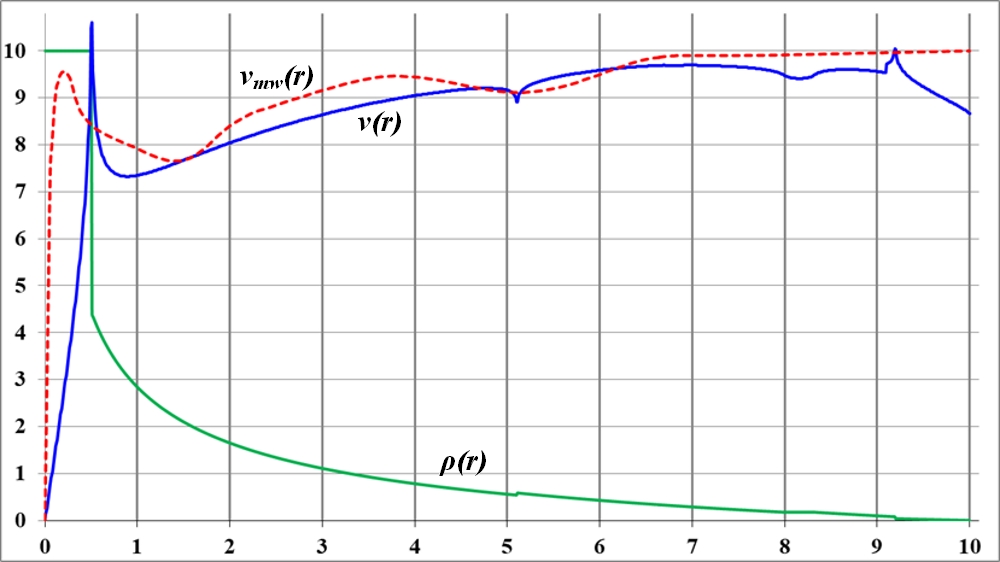
Рис. 2.8. Плавный изгиб, переход на графике плотности ведёт к такому же плавному изгибу на кривой вращения

Просматривается закономерность: скачки плотности всегда приводят к появлению пиков на кривой вращения. Напротив, плавный переход на функции плотности приводит к такому же плавному изгибу кривой вращения. Для новой проверки делаем в области r = 5 параболическую выпуклость на функции плотности. С полученной функцией плотности фрагмент кривой вращения приобрел вид

Рис. 2.9. Плавный параболический изгиб на графике плотности привёл к значительному, но плавному изгибу на кривой вращения

На графике видно, что в точке излома функции плотности на кривой вращения также образуется заметный излом. Но плавность изменения функции плотности по-прежнему приводит к плавному изменению кривой вращения. При этом можно предположить, что на интервале неизменности функции плотности кривая вращения растёт. Общая тенденция к уменьшению значения плотности ведёт к такому же уменьшению и величины скорости на кривой вращения.

3. Подбор функции плотности

Можно отметить, что использование гладких аналитических кривых для функции плотности даёт сглаженное, плавное приближение к кривой вращения Млечного Пути, её графику, формирует достаточно плавную кривую на всём её протяжении. Иначе говоря, переменная плотность позволяет получить кривые вращения с различным уклоном. Таким образом, следует предположить, что можно построить кривую вращение любой формы, в том числе, и максимально похожую на кривую вращения галактики Млечный Путь. В самом деле, спиральный диск галактики вполне можно рассматривать как сплошной, но имеющий переменную плотность вещества.

Проведенные вычисления достаточно отчётливо показали такую возможность корректировки кривой вращения изменением функции плотности. Однако сложность подбора функции плотности, в свою очередь, показала, что для дальнейших построений требуется разработать какой-то механизм, процедуру, облегчающие формирование функции плотности.

Функция плотности, как и все графики на диаграммах, в наших вычислениях состоит из 1000 точек, поэтому изменить их все вряд ли возможно и необходимо. Поэтому мы делим весь интервал функции на 10 участков, на которых криволинейный график функции плотности заменяем прямыми линиями. Использование вместо прямых линий парабол или гипербол оказалось неоправданно сложным, поскольку в некоторых случаях изломы сохранялись и даже возникали неестественные отклонения.

Изменения производим в узлах этих прямолинейных участков, в точках излома, соединения линий. Используем 11 точек, совпадающих с линиями сетки графика: r₀, r_0,5, r₁…r₁₀. Графику плотности в начальной части присваиваем ещё один параметр — значение максимума, пика графика.

Каждый участок задаём координатами начала и конца (x_нy_н — x_кy_к). Уравнение линии определяем по этим точкам. Сначала находим коэффициент наклона прямой

Свободный член находим из первого уравнения

Система уравнений для построения обобщенно имеет вид

В первом варианте на начальном интервале мы использовали параболическую кривую, подобранную ранее. Для формирования рабочей функции плотности была использована исходная функция плотности (2.1), график которой после аппроксимации отрезками прямых приобрёл следующий вид

Рис. 3.1. Исходная функция плотности

Используя этот график плотности диска, до его коррекции строим исходную кривую вращения.

Рис. 3.2. Кривая вращения по исходной функции плотности

Отмечаем, что кривая вращения явно, сильно отличается от кеплеровской. Теперь вносим изменение в функцию плотности. Для начала корректируем точку x₁

Рис. 3.3. Кривая вращения после деформации исходной функции плотности

Изменение кривой вращения видны достаточно отчётливо. Напомним, что нас интересует функция плотности, приводящая к кривой вращения нашего диска, подобной наблюдаемой кривой вращения галактики Млечный Путь. Последовательно, интуитивно вносим изменения в другие точки функции плотности. График формируемой кривой вращения заметно приближается к кривой вращения галактики.

Рис. 3.4. Первое приближение кривой вращения к эталону

Поскольку пик кривой вращения диска был заметно смещён вправо от пика кривой вращения галактики Млечный Путь, мы увеличили пик плотности диска до 50. Смещение уменьшилось. На следующих рисунках приведены результаты других последовательных эмпирических приближений, подгонки функции плотности

Рис. 3.5. a)…д) — последовательные приближения кривой вращения v(r) диска к эталону — кривой вращения v_mw(r) галактики Млечный Путь

На рис. 3.5а)…д) приведены кривые вращения диска и соответствующие им функции плотности, полученные в результате их последовательной деформации. Кривые вращения заметно приблизились к кривой вращения галактики Млечный Путь. Пробуем ещё точнее сблизить графики. Заключительный этап такого подбора приведён на следующем рисунке. Как видим, кривая вращения диска выглядит довольно близкой к наблюдаемой кривой вращения галактики Млечный Путь

Рис. 3.6. Подобранная функция плотности ρ(r) и соответствующая ей кривая вращения v(r) приемлемо, максимально совпадающая с эталонной, наблюдаемой кривой вращения v_mw(r) галактики Млечный Путь

Результат, совпадение кривых вращения на рис. 3.6 следует признать хорошим. Некоторые специфические отклонения в начале и конце кривых можно объяснить. На начальном этапе достичь хорошей точности не позволяет дискретность графика. Первые 10 точек выводятся с погрешностью от 10 до 200 %. Например, различия между первым и вторым шагами двукратные. В конечной точке график кривой вращения диска связан со сложностью подбора функции плотности. Интервал слишком длинный для достаточно подробной детализации функции.

Вместе с тем следует учесть и ещё одно немаловажное обстоятельство: аппроксимируемая наблюдаемая кривая вращения галактики Млечный Путь сама построена с довольно большой погрешностью.

Из проведённых вычислений можно сделать вывод. Следует признать принципиальную возможность формирования такой функции плотности диска, изменения его радиальной плотности, которая позволяет получить любую заданную наперёд форму кривой вращения. В частности, сформированная выше вполне реальная функция плотности диска позволяет получить кривую вращения, предельно совпадающую с наблюдаемой кривой вращения галактики Млечный Путь. Следовательно, существуют такие же функции плотности диска, соответствующие кривым вращения других галактик.

Что непосредственно касается взятой за эталон галактики Млечный Путь, то построить для неё фактическую функцию плотности, видимо, технически возможно. Судя по всему, необходимые для вычислений основные параметры всех её составляющих известны: координаты звёзд и их массы. Вполне возможно построить график сил, действующих на некоторую звезду, параметры движения которой, предположительно, не соответствуют законам Кеплера. Понятно, что для этого потребуется произвести вычисления её силовых взаимодействий с несколькими миллиардами остальных звёзд галактики. Такие вычисления являются эквивалентом расчётов по плотности, причём в них усреднённая плотность представлена в точном дискретном виде, в виде пар звезда-звезда. Серьёзную трудность при таких расчётах составит, видимо, учёт масс газопылевых объектов. Вычисленная сила для проблемной звезды даст точное значение её фактической скорости, соответствует ли она её устойчивому орбитальному движению.

4. Функция массы диска М(r)

Помимо кривой вращения функция плотности позволяет построить также и график распределения массы объекта. Проведём сравнительный анализ поведения массы диска, сравним аналитическое и численное интегрирование функции массы: как зависит полная и частичная масса диска от функции его плотности. Исследуемый диск имеет в общем случае переменную радиальную плотность, зависящую от удалённости от центра. В случае переменной плотности дифференциал массы, масса элементарного участка диска определяется в следующем виде

Найдём частичную массу диска, его внутренней дисковой части некоторого радиуса Rx, то есть, радиальное распределение массы. Эта масса, очевидно, нарастающая, чем больше радиус Rx, тем больше масса. Используя дифференциал (4.1), массу можно найти интегрированием, указав радиус диска R₀ в качестве верхнего предела интеграла по радиус-вектору

Замечаем, что подынтегральная функция не зависит от угла, что не удивительно, поскольку мы изначально установили угловую симметрию. Поэтому сразу же вычисляем интеграл по этой переменной

Рассмотрим три принципиальных случая, определяемых законом изменения плотности. Первый случай, который можно назвать кеплеровским, — вся масса диска находится в его центре, плотность диска — "пиковая" ρ(0)= ρ₀. Численное интегрирование даёт такой вид функции массы

Рис. 4.1. При нахождении всей массы в центре диска массы M(r) всех частичных, вложенных дисков равны этой массе

В этом случае масса каждого частного диска одна и та же и равна массе, находящейся в его центре. Для наглядности и удобства вычислений интеграл в общем виде (4.2) для этого случая желательно изменить, а точнее, разделить на два интеграла. Масса такого диска сосредоточена в его центре и, очевидно, имеет некоторый минимальный объём, радиус r₀. В остальных точках плотность равна нулю, поэтому

Масса не зависит от радиуса частичного диска и всегда равна M₀. Результаты численного и аналитического интегрирования, как видим, совпали.

Второй принципиальный случай — плотность диска неизменна по всему его объёму, радиусу

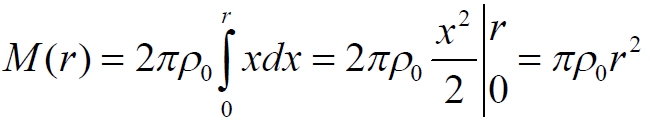
Итог аналитического интегрирования означает, что при такой однородной плотности каждый промежуточный диск имеет массу, пропорциональную квадрату его радиуса. Численное интегрирование также показало на диаграмме параболу, то есть, графический результат совпал с аналитическим

Рис. 4.2. В однородном диске массы всех частичных, вложенных дисков растут пропорционально квадратам их радиусов

Третий случай относится к функции плотности, приводящей к распределению массы, похожей на гиперболическое распределение масс в дисковых галактиках. Рассмотрим вариант гиперболического уменьшения плотности, установив, что в нулевой точке, в центре галактики плотность равна ρ₀

Отметим, что логарифмическая добавка к радиусу заметно меньше самого радиуса, поэтому график выглядит практически как прямая линия. Например, при r = 1000 добавка составляет чуть меньше 7. Фактически масса промежуточных, частных дисков такой галактики растёт пропорционально их радиусу, а его логарифм не вносит практически никаких корректив

Рис. 4.3. В диске с гиперболически уменьшающейся от центра к периферии плотностью, массы всех частичных, вложенных дисков растут прямо пропорционально их радиусам

Эти три принципиальных, наглядных варианта рассматривают простейшие аналитические (не табличные) функции плотности. Рассмотрим теперь массу диска с табличной формой функции плотности, подобранной ранее под кривую вращения галактики Млечный Путь.

Рис. 4.4. Распределение массы диска с функцией плотности ρ(r), подобранной под наблюдаемую кривую вращения v_mw(r) галактики Млечный путь

График показывает величину массы частичного диска, заключенной в круге соответствующего радиуса. Полная масса диска на рисунке равна 10. Отметим её некоторые особенности. Вблизи центра диска, области, имеющей предельную плотность, сосредоточена всего лишь десятая часть его полной массы. Действительно, плотность в пике этой части равна 50, то есть, почти в 100 раз превышает плотность на половине радиуса диска, равную 0,5. Масса половины диска по радиусу составляет всего 65 % от общей массы. Напротив, половина массы диска сосредоточена в пределах радиуса 40 %.

Всё это может показаться странным: часть диска с малой плотностью весит больше, чем его часть с существенно большей плотностью. Однако странность легко объяснима. Более плотная часть диска занимает существенно меньший объём. Менее плотная масса составляет, по сути, основную часть диска, его массы.

Выводы

В наших вычислениях мы не рассматривали диск как полный аналог какой-либо галактики. Тем не менее, то, что его кривую вращения удалось достаточно точно приблизить по форме к кривой вращения галактики Млечный Путь, свидетельствует о возможности формирования любой кривой вращения галактики, любой галактики исключительно за счёт специфического распределения её внутренней массы. То, что возможно для абстрактного, но физически возможного объекта, несомненно, должно быть возможно и для физического объекта реального.

Для достижения поставленной цели — формирования заданной формы кривой вращения — мы не использовали никаких внешних, скрытых сил или субстанций. Все без исключения "странности", возникшие в процессе вычислений, не являются противоречиями, все они нашли логическое объяснение.

Оглавление

1. Сила притяжения внутри диска

2. Построение пробных диаграмм

3. Подбор функции плотности

4. Функция массы диска М(r)

Выводы