Силы тяготения внутри обруча, сферы и между двух точек [Петр Путенихин] (fb2) читать постранично, страница - 3

от относительного положения тела m, но от радиуса самой сферы – нет. Фактически это означает, что сила притяжения тела одна и та же, каким бы ни был радиус сферы – 100 метров или 100 световых лет. Однако это кажущаяся странность. Мы задали для сферы поверхностную плотность, а она и определяет общую массу сферы, которая однозначно зависит от радиуса сферы. Хотя в маленькой сфере силы создаются её малой массой, а в большой сфере – большой, расстояния также имеют соответствующие величины, это и ведёт к независимости сил от радиуса сферы.

Рассмотрим два граничных случая: тело m находится в центре сферы k = 0 и на её поверхности k = 1. Первый случай

Результат ожидаемый, в центре сферы тело находится в состоянии невесомости. Второй случай

Это табличный интеграл

Результат также ожидаемый: тело на поверхности сферы обязательно будет испытывать силу притяжения.

Рис.2.3. График изменения силы притяжения внутри сферы пробного тела в зависимости от его удалённости от центра

Результат ожидаемый и объяснимый. Этот же график с логарифмической шкалой

Рис.2.4. Логарифмический график изменения силы притяжения внутри сферы пробного тела в зависимости от его удалённости от центра

Интеграл силы (2.3) мы формировали исходя из положительного направления силы в сторону центра сферы. Интегрирование и графики показали положительное значение силы. Из этого следует вывод: тело в пустой сфере притягивается к её центру так, будто там находится некий массивный объект.

Проблема трактовки притяжения тела внутри сферы

В исходном варианте статья начиналась словами "Известно, что тело внутри полой сферы…". Однако в процессе исследований эта часть фразы была заменена на "Считается, что тело внутри полой сферы…". Эта замена связана с обнаруженным противоречием. В результате наших исследований мы пришли к выводу, что тело внутри полой сферы испытывает силу притяжения со стороны этой сферы, хотя, по мнению других авторов, такой силы нет. Вывод об отсутствии силы притяжения внутри сферы достаточно полно изложен, по меньшей мере, в трёх работах [1, 2, 3]. Понятно, что два взаимно исключающих вывода не могут быть верными одновременно. Один из них ошибочен.

Наши выводы опираются на строгое математическое доказательство. По сути, они – строго доказанная математическая теорема. Следовательно, ошибочным является мнение об отсутствии силу внутри сферы. В чём именно состоит ошибка? Рассмотрим, как получен этот ошибочный вывод на примере работы [3]. Заметим, что, по сути, эту работу можно считать если не перепечаткой, то близкой по тексту к более ранним работам [1, 2].

Рассмотрен шар радиусом R, на поверхности которого находится галактика A. Этот шар с галактикой опоясан шаровым слоем толщиной h. Приводится доказательство того, что на галактику A со стороны этого слоя не оказывается никакого гравитационного действия, притяжения. Другими словами, в однородной Вселенной на эту галактику все другие галактики, вне этого шара не оказывают никакого влияния.

Рассматриваются силы притяжения, действующие на галактику A со стороны галактик, расположенных в этом слое в противоположных от неё направлениях, в объёмах элементов слоя V1 и V2. До этого момента рассуждения вполне корректны. Однако уже следующее утверждение является грубой ошибкой. При сравнивании объёмов элементов утверждается, что их угловые площади S1 и S2 и, соответственно, объёмы пропорциональны квадратам расстояний от галактики до поверхности слоя – r1 и r2. Приводится рисунок, на который мы сразу же добавили неравенство сил

Рис.2.5. Копия рисунка из работы [3]

и уравнение к нему

Автор допускает, вообще-то, очевидную небрежность, ошибку – это уравнение неверно. В нём проводится отождествление трёх разных сфер, имеющих радиусы R, r1 и r2. Каждая из площадей, дифференциал площадки, бесконечно малый участок на сфере определяется уравнением

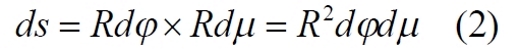
где φ и μ – полярные углы сферического сегмента.

Каждый из этих полярных углов имеет вершину в начале своих собственных полярных координат. Только при этом условии площадь на поверхности сферы определена уравнением (2). В рассмотренном случае (1), эти начала полярных координат разные, поэтому, например, для S1 мы обязаны записать

Считая, что полярные углы φ и μ для всех трёх сфер одинаковы, каждая из площадок, дифференциал площади, например, в (3) это S1, обозначена с "точки зрения" соответствующих сфер: сферы с радиусом R и началом координат в центре этой сферы, и сферы с радиусом r1 и началом координат в точке А. Но эти две площадки